算法分享:堆排序
堆排序基本概念
堆的结构可以分为大根堆和小根堆,是一个完全二叉树,而堆排序是根据堆的这种数据结构设计的一种排序,
首先介绍什么是大根堆和小根堆
性质:
-
大根堆:每个结点的值都大于等于其左孩子和右孩子结点的值。

大根堆映射的数组为:

-
小根堆:每个结点的值都小于等于其左孩子和右孩子结点的值。
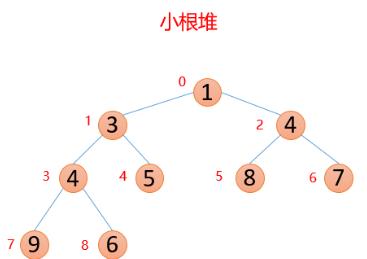
小根堆映射的数组为:

注:与搜索二叉树不同,没有要求说大根堆中一定要小的值在左边,大的值在右边。
基本概念:查找数组中某个数的父结点和左右孩子结点,比如已知索引为i的数,那么
-
父结点索引:(i-1)/2(这里计算机中的除以2,省略掉小数)
-
左孩子索引:2*i+1
-
右孩子索引:2*i+2
所以上面两个数组可以组成堆结构,因为他们满足堆的定义性质:
大根堆:arr(i)>arr(2*i+1) && arr(i)>arr(2*i+2)
小根堆:arr(i)<arr(2*i+1) && arr(i)<arr(2*i+2)
堆排序基本思路:
以将无序数组构造成大根堆为例:(其中升序用大根堆,降序就用小根堆)
-
首先将待排序的数组构造成一个大根堆,此时,整个数组的最大值就是堆结构的顶端
-
将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为n-1
-
将剩余的n-1个数再构造成大根堆,再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序数组
图例可查阅参考资料
参考资料: